The cannabis industry has a problem. Like in most areas of society and industry, inflation has been causing issues for dispensaries and growers around the country, but unlike in many areas, raising the prices for weed comes with risks. If you raise prices but the dispensary down the road doesn’t, what will your customers do?
Well if they’re struggling financially, they’ll switch stores in a heartbeat. If neither of you raise prices, you’ll both share the customers but inflation will eat into – or completely devour – your profits. If you both raise prices, then you can get the best of both worlds, but that opens up the risk that your competitor will undercut you. If you know anything about game theory, you might recognize this as a Prisoner’s Dilemma. But what does that mean, and can we use the underlying theory to solve the problem facing the weed industry?
TL;DR
- Inflation is hitting the cannabis industry just like it is in every sector, but state-wide competition makes it risky for dispensaries to raise prices.
- Our survey on inflation and cannabis suggested that about half of dispensary customers would buy less weed if prices increased.
- Game theory is an attempt at a “science of strategy,” involving analyzing “games,” where the outcome depends on the actions of all of two or more players.
- The dispensary inflation pricing problem can be modeled as a prisoner’s dilemma:
- Both parties raising prices is the best mutual outcome
- Both keeping low prices is OK but really not great
- One raising while the other doesn’t means all the benefit for one and none for the other.
- In a prisoner’s dilemma where there are multiple “rounds,” simple “tit for tat” is the best strategy. They betray; you do the same next time. They cooperate; you do the same next time.
- Although you can’t explicitly agree with your competition to raise prices (that’s a cartel) you can still use game theory to elicit cooperation.
- A “price match guarantee” models tit-for-tat in pricing. You raise your prices, but agree to match any price from a competitor.
- This removes the benefit of keeping low prices (since you immediately match) while externally signaling a sustainable price.
Inflation and Cannabis: Why Dispensaries and Growers Are Struggling

In our report on inflation and the cannabis industry, we outlined the problem dispensaries and growers are facing in detail. The basics are very straightforward, though. Inflation is boosting costs for growers and dispensaries like it is in many other areas. For example, the fuel to take the product from the growers to the dispensaries, the cost of fertilizer and many other similar expenses have risen, eating into profits and making it unsustainable to continue selling eighths at the same price.
This would all be OK (if not ideal), but there is a lot of competition in states like Colorado, with more mature markets and tons of growers and dispensaries in the state. With an abundance of in-state supply, if you raise prices it’s easy for dispensaries to buy from different growers and for customers to buy from different dispensaries. This basically paralyzes businesses, especially those where losing customers could lead to serious financial trouble pretty quickly. Keeping prices low slows the loss of profits, but the loss is still happening, one way or the other.
This is the “weedflation” problem in a nutshell. There is a very real – and not entirely inaccurate, according to our survey – perception that raising prices would turn customers off pretty quickly. And the competition is always ready to take your poorer customers on.
A Lightning Introduction to Game Theory
Game theory is a framework to describe scenarios involving competing players, particularly when the outcome for one player depends on the choices of the other players as well as those of the original player. The situation is described as a “game,” which is basically any collection of circumstances in which the result depends on the actions of two or more players. The players are understood to be “rational” decision-makers, meaning that they are expected to make decisions that will maximize the benefit to them (the “utility,” to be precise).
By analyzing such situations, game theory aims to develop a “science of strategy,” or at least come up with ways for decision-makers in such situations to make the most optimal decisions.
The Prisoner’s Dilemma
The most well-known example of game theory is the prisoner’s dilemma, and it’s a really good way to understand what exactly the above description actually means. The dilemma goes like this: two prisoners have been arrested for robbing a bank and put in separate cells (so communication between them is impossible). However, there is no hard evidence they committed the robbery. But the prosecutor has a plan: he tells each prisoner that if they confess and the other doesn’t, he will drop all charges against them and use the testimony to convict the other. If both of them confess, he says he’ll give them early parole and less of a sentence than either would get individually. If neither confesses, he will have to settle with a much lower charge of firearms possession and both will get less time.
Now, imagine you’re a prisoner in this situation. What should you do? It seems like it’s safer to confess right off the bat. Imagine your accomplice doesn’t confess: if you don’t confess either, you’ll get the punishment for firearm possession, but if you do you’ll get off with no punishment. Now imagine that your accomplice does confess: if you don’t confess, you’ll get the biggest sentence possible, but if you do you’ll only get a smaller sentence. In both cases, confessing leads to better outcomes.
These decisions are often placed in a grid to make the interactions more clear. Here we’ll put figures on the sentences to make it easier: 10 years for full punishment, 5 years for reduced and 2 years for just the firearms charge.
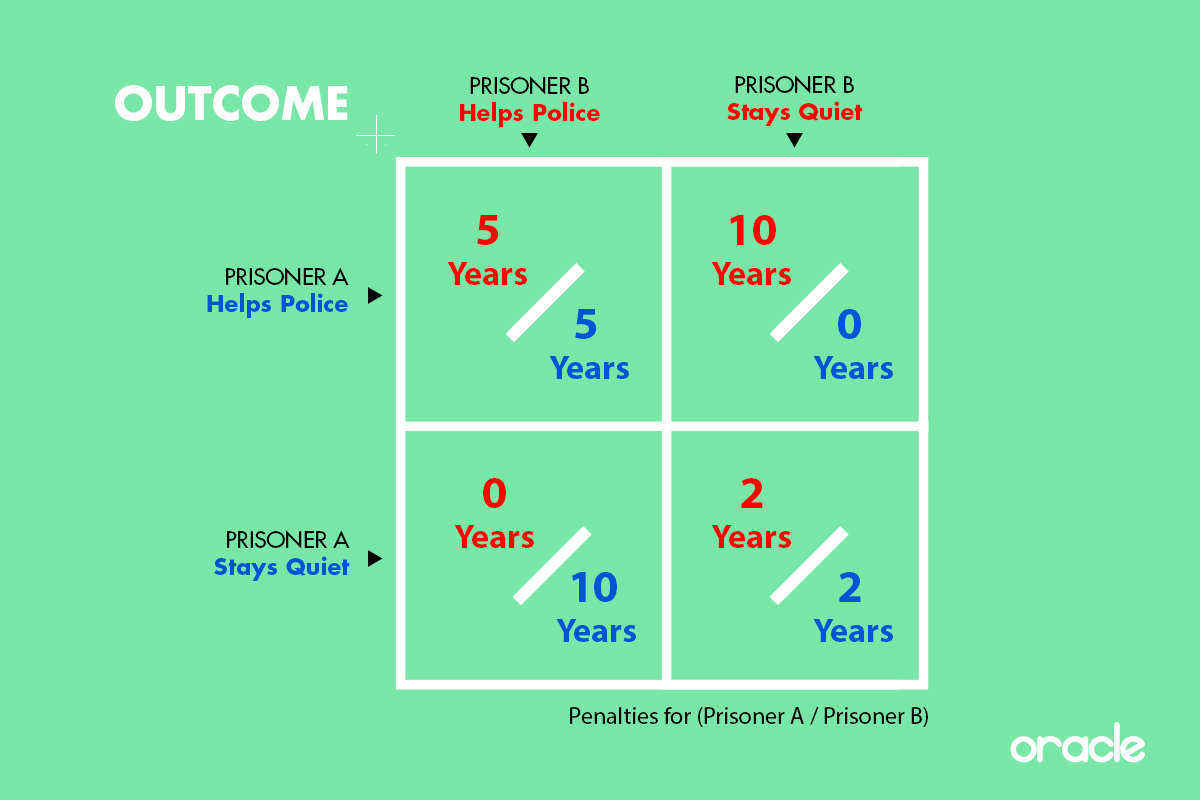
It’s clear from this that the most mutually beneficial option is for neither to confess. But the genius of the prosecutor is giving a big incentive for confessing. These people have to be considered to be acting in pure self interest, so the best outcome for either person is confessing while their accomplice doesn’t. But the outcome completely depends on what the other party does.
The “dilemma” really comes in here: your opponent will reason exactly the same, so they will also benefit more by confessing. This means that you’ll both get 5 years if you act in pure self interest, but you’d just get 2 if everyone cooperated. However, the rules of the game demand that confessing is the more rational choice, regardless. If you try to cooperate but your opponent acts rationally, you will get 10 years. So you can’t really deviate from this choice without a huge risk. If they could communicate with each other, they might be able to mutually agree not to confess (although this still depends on trust). However, in the dilemma this isn’t possible, and you’re left with the contradiction: self-interest demands that both confess, yet it’s clear that the opposite choice would be more mutually beneficial.
Game theory involves working out what the best thing is to do in this and similar situations. Based on this, you might think the practical applications were pretty limited – after all, what the hell type of prosecutor would do something like this? – but actually it has many applications.
Weedflation as a Prisoner’s Dilemma
The problem dispensaries are having through inflation can be considered a prisoner’s dilemma just like the example above. The situation basically works in the same way: if one dispensary adjusts prices for inflation, but the other keeps it low, the one with the lower prices will take up all the business. If both leave prices as they are, then sales will be spread equally but not making much – if any – profit for either. If both increase together, then sales will be evenly distributed – albeit probably reduced in volume – and both will be making profit. As a grid, it looks like this:
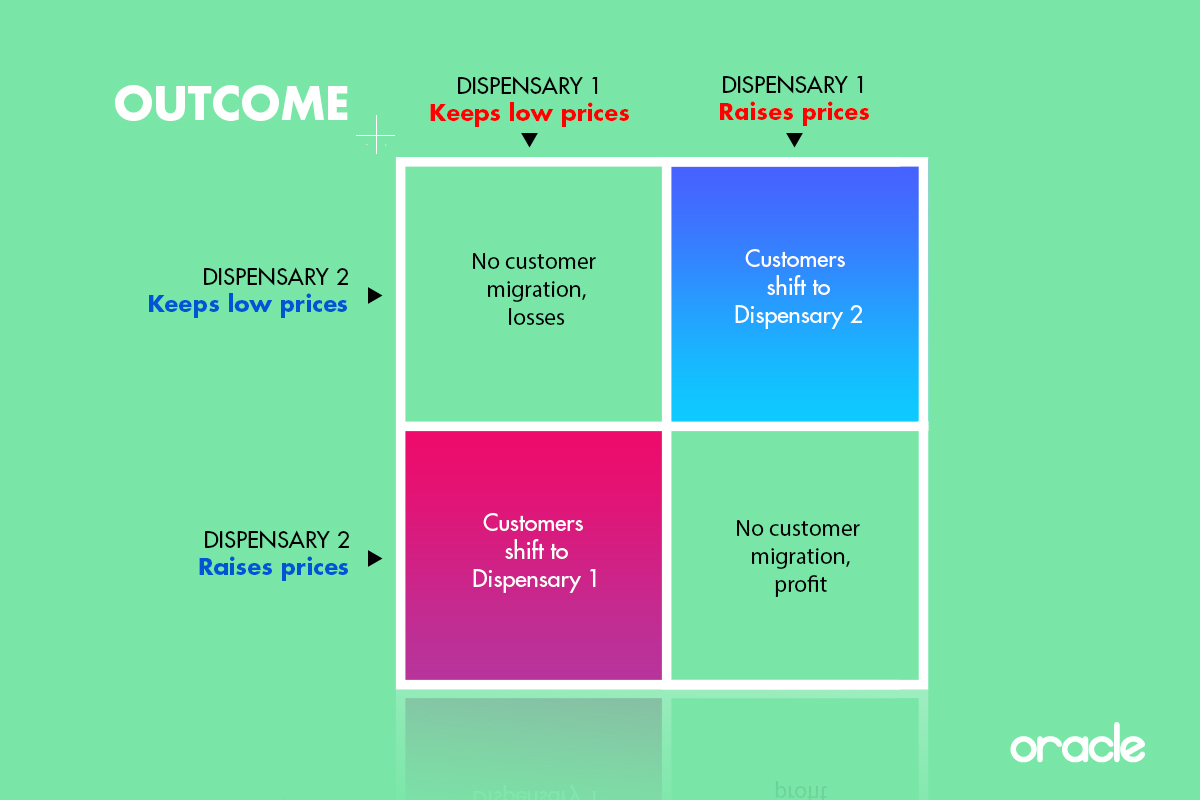
Of course, this simplifies things to some extent. Things like intelligent pricing strategies and customer loyalty will affect how people respond to different approaches to inflation price increases. However, the assumptions are pretty reasonable if you treat the customer as a “rational” actor that will attempt to get his or her weed at minimal cost. With this in mind, the form of the prisoner’s dilemma becomes very clear. If one takes action but the other doesn’t, there is a huge potential gain, if both try to screw the other over (by keeping unsustainably low prices) then they both suffer, but if both cooperate to raise prices, then both will stay in profit.
The remaining simplification is that this would have to take place in a town with only two dispensaries. In reality, the “game” will have many, many more players but the price of non-cooperation will remain the same to some extent. One dispensary could benefit at the expense of all others.
Initial Solutions and the Challenge of Iteration
The bad news for people hoping for cooperation in situations like this is that game theory suggests it’s a bad strategy. As described above, any analysis of what you should do as an individual settles on confessing as being the most “rational” choice in a purely self-interested way. No matter how much you can argue that refusing to confess makes more sense, when push comes to shove and the choice is made behind closed doors, unavoidable logic pushes players to confess.
This forms a “Nash equilibrium” in the game. This basically means the choice that each person would stick to even if they knew their opponents’ move. It’s kind of like a “steady state” for these problems. If you confess, you wouldn’t change your mind if you knew your opponent was also going to confess (since you’d get five extra years if you didn’t confess), and you wouldn’t change it if you knew your opponent wouldn’t confess (since you’d go from getting no punishment to getting two years). The logic works for your opponent too, and so confess-confess is an equilibrium point.
However, what happens if you don’t just play once? A more realistic situation is an “iterated” prisoner’s dilemma, which basically means one with multiple “rounds” of the same game, where the players remember the other’s actions from the previous rounds. This is more like our dispensary example: if you raise prices but your competitor doesn’t, you can always change them back tomorrow. But this changes the situation substantially. Betrayal today will be met with retaliation tomorrow. It’s also possible to continuously cooperate through multiple iterations, building trust along the way.
Solving the Iterated Prisoner’s Dilemma
Working out the best solution in this situation is much more difficult, and a lot of effort has been expended to get to the bottom of it. In the finite case, where you only play the game a pre-determined number of times (and you know the number), you end up with the same as the above. Whatever round number the game will end on, in the last game you might as well betray because there will be no consequence and it’s the best single-game move. But then you know that your opponent will be thinking the same thing, so they’ll definitely betray you too. So then the last round is a foregone conclusion, and the last chance for consequences is the second-to-last game. However, since this is now the final “real” game, the same conclusion emerges here for the same reason, you go the third-to-last game and on and on until the whole thing unravels into mutual betrayal the whole way through.
For games with an indefinite number of rounds, you can never be sure when the last one will be. This makes cooperation more likely because any betrayal could be met with consequences next time. When Robert Axelrod investigated this through an open competition, he found that the winning strategy was “tit for tat.” This means that, after cooperating in the first game, the player simply repeats the previous move of the opponent. Despite a competition full of complex and ingenious strategies, the winning code was written in just four lines of BASIC. He even had another round of the competition afterwards, where everybody who entered knew what happened in the first one, and tit for tat won again.
The key to doing well lies not in overcoming others, but in eliciting their cooperation.
Robert Axelrod, PhD, Professor of Political Science and Public Policy at the University of Michigan
Axelrod really brought attention to the iterated prisoner’s dilemma and did a good job of breaking down the necessary components of a successful strategy. These were:
- Nice: The strategy has to be “nice,” in that it shouldn’t be the first of the players to defect. In other words, it should be optimistic.
- Retaliating: It has to retaliate, because if it’s simply always nice it can be exploited by nastier strategies.
- Forgiving: This basically means that the retaliation has an end. If the opponent switches to cooperating, then the strategy should “forgive” to avoid getting stuck in a cycle of betrayal.
- Non-envious: The goal shouldn’t be to get a better outcome than the opponent.
Axelrod’s conclusion is well worth keeping in mind, as he summarizes the key lesson of the competitions (emphasis added):
“There is a lesson in the fact that simple reciprocity succeeds without doing better than anyone with whom it interacts. It succeeds by eliciting cooperation from others, not by defeating them. We are used to thinking about competitions in which there is only one winner, competitions such as football or chess. But the world is rarely like that. In a vast range of situations, mutual cooperation can be better for both sides than mutual defection. The key to doing well lies not in overcoming others, but in eliciting their cooperation.”
Solving Weedflation With Game Theory: What We’ve Learned
So with the lessons of the previous section in mind, we can turn back to the “weedflation” problem facing growers and dispensaries. Here, to be clear, cooperating means raising prices to a sustainable level to cope with inflation, and defecting means keeping prices low to undercut the competition. If the decision only had to be made once, mutual defection would be the logical (although not the best) choice, as the Nash equilibrium point would suggest.
However, in practice, the weedflation problem is an iterated prisoner’s dilemma with no pre-defined end. As such, cooperation is much more likely to emerge eventually than it would be otherwise. The challenge is that the same motivations are there: if your competitors raise prices but you don’t, you benefit greatly. This fear is what prevents positive change in the situation, “if I raise but they don’t, I’m screwed.” But they are looking at you, not raising your prices, and seeing the same justification for maintaining the status quo.
The first characteristic Axelrod identified, being “nice,” is key here. The winning strategy was tit for tat, but with cooperation as a first move. So, as much as it might not seem wise, the best thing to do according to game theory is to raise your prices to a level where you would be making enough on each eighth. Even better, you could encourage your competitors to do the same through explicit cooperation – gather up business and discuss raising prices together. Then the next step suggested by pure theory is to wait: hopefully, your competitors will see that you raised prices and start considering whether they could do the same. The difference from a “pure” prisoner’s dilemma is important here: everyone is struggling if we stick to the status quo, so your competitors actually want to increase prices if they can.
However, if they don’t increase prices too, game theory suggests you should consider lowering yours again (through a limited-time sale, for instance) to remain competitive. Of course, switching prices back and forth isn’t ideal, but as Axelrod points out, the goal is actually to elicit cooperation, and refusing to let competitors steal your customers so easily is an important part of that. You can’t offer someone an easy win because they might just take it.
Finally, if (hopefully when) your competition increases prices, you can raise your in line with it too. Because you need to be “forgiving” even if the competition tried to screw you at an earlier stage. The more dispensaries you get on your side with this approach, the better. As long as you can make a living, you’re “winning” – don’t worry if another company is making more.
“What, Isn’t That a Cartel?” – Building a Real-World Strategy With Game Theory
Although we’ve sketched an approach above, there is a very big problem with what we’ve described above. Explicitly planning to raise prices in tandem with your competitors is what’s technically known as a cartel. This is – rightfully – illegal in the US due to anti-trust laws. And also, let’s be real, it would not be a good look for a legal weed industry even if it wasn’t.
So what is the real-world solution?
While anti-trust laws may make it difficult to directly communicate about pricing with your competitors, there is an alternative that hits on all of the key points identified by Axelrod. This is deceptively simple, too: raise your prices, but include a price-match guarantee.
This has everything we’re looking for:
- Nice: You raise prices immediately, so you take the cooperative act first without waiting for anybody to act.
- Retaliating: If your competitors don’t increase prices, their price automatically becomes your price and so there is an immediate consequence for non-compliance.
- Forgiving: Your prices rise immediately when competitors raise theirs. There is no “punishment” period after competitors re-adjust.
- Non-envious: Finally, it’s not a “lowest price” guarantee, it’s a matching guarantee. By definition, this isn’t trying to “win,” it’s trying to remain competitive.
You can see how this plays out if you think through an example. Imagine a town has three dispensaries, all charging $20 / eighth. One of these dispensaries (High Prices) raises their prices to $25 / eighth to cope with inflation, paying their increased costs while still making a small profit on each bag. Importantly, they also institute a price match guarantee. The other dispensaries notice the changes, and one (Should Be Higher) sees an opportunity to inch their price up a little, reaching $22 / eighth, while the other (Rock Bottom) keeps their prices the same.
Customers notice the price increase too, and some switch to Rock Bottom in response. However, the price match guarantee means that High Prices doesn’t lose that much customers. In fact, the customers who tried Rock Bottom after the price rise know they can get the same deal at High Prices anyway, so switch back pretty soon. Note that High Prices is stuck with $20 / eighth while the situation is like this, despite the ticket price being higher. Meanwhile, Should Be Higher is losing some customers to Rock Bottom but still doing OK because each sale meets their costs more and they still don’t look super expensive. However, noticing the issue, they also add in a price match guarantee. Sometimes they lose a couple of bucks because of the deal, sometimes they don’t.
Now Rock Bottom starts to notice that they aren’t doing so great despite having the lowest prices in town. The price match guarantees are taking away their advantage, and even when they do get customers, the sales are barely enough to keep the dispensary lights on. Eventually, they realize that if they can’t increase their customer base with low prices, they might as well make more per purchase. They, like High Prices, put prices up to $25 / eighth with a price match guarantee.
Should Be Higher is the remaining hold-out. However, both High Prices and Rock Bottom are now matching their $22 / eighth, while signaling a sustainable price outwardly. Customers are getting increasingly used to the higher prices and are essentially paying the same everywhere. There is no benefit to Should Be Higher for having the lowest prices; all they’re doing is making it harder for all three companies to stay in profit. Finally, they cave and increase to $25 / eighth.
Of course, this is a hypothetical situation and things would likely be a little messier than this. But the key elements of a successful strategy are all there and it’s likely that self-interest would lead all companies to increase their prices in the end. It levels the playing field in terms of sales volume while sending the message to “raise prices” to any competitors. This isn’t a cartel; this is market forces and pricing strategies pushing people to make the logical decision in the end.
Conclusion: Learning to Game the Market
“Weedflation,” like inflation, is likely to remain an issue for a little while and it’s certain to come back again in the future. However, by framing the problems faced by dispensaries as a prisoner’s dilemma, game theory – and the many experiments that have taken place over the years – offers a solution. By being flexible on your price, you can meet your competition “tit for tat,” maximizing your selling price while removing any benefit for competition that would undercut you. So if you’re a dispensary concerned about raising your prices, at least you know how game theorists would approach the situation.
